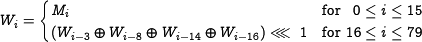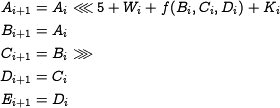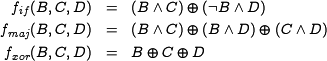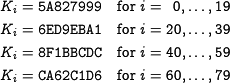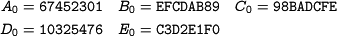Difference between revisions of "SHA-1"
(→Message Expansion) |
(→State Update Transformation) |
||
| Line 31: | Line 31: | ||
==== State Update Transformation ==== | ==== State Update Transformation ==== | ||
| + | |||
| + | The state update transformation starts from a fixed initial value | ||
| + | ''iv'' for 5 32-bit registers <amsmath>$A,B,\dots,E$</amsmath> (also | ||
| + | referred to as state variables) and updates these registers in 80 | ||
| + | steps (<amsmath>$i = 0,\dots,79$</amsmath>) by using the word <amsmath>$W_i$</amsmath> and the step | ||
| + | constant <amsmath>$K_i$</amsmath> in step <amsmath>$i$</amsmath>. One step of the state update transformation is defined as | ||
| + | |||
<amsmath> | <amsmath> | ||
\begin{equation*} | \begin{equation*} | ||
| Line 41: | Line 48: | ||
\end{aligned} | \end{aligned} | ||
\end{equation*} | \end{equation*} | ||
| + | </amsmath> | ||
| + | |||
| + | The function <amsmath>$f$</amsmath> depends on the step number: steps <amsmath>$i=0,\dots,19$</amsmath> use the ''IF-function'' referred to as <amsmath>$f_{if}$</amsmath> and steps <amsmath>$i = 40,\dots,59$</amsmath> use the ''MAJ-function'' referred to as <amsmath>$f_{maj}$</amsmath>. The | ||
| + | remaining steps, use a 3-input XOR referred to as <amsmath>$f_{xor}$</amsmath>. The Boolean functions are defined as follows: | ||
| + | |||
| + | <amsmath> | ||
| + | \begin{eqnarray*} | ||
| + | f_{if}(B,C,D) &=& (B\wedge C) \oplus (\neg B\wedge D) \\ | ||
| + | f_{maj}(B,C,D) &=& (B\wedge C) \oplus (B\wedge D) \oplus (C\wedge D)\\ | ||
| + | f_{xor}(B,C,D) &=& B \oplus C \oplus D | ||
| + | \end{eqnarray*} | ||
</amsmath> | </amsmath> | ||
Revision as of 09:47, 12 October 2006
Contents
1 General Description
SHA-1 is an iterated hash function. It can be used to
compute a 160-bit hash value for messages having a length of less
than 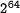 bits, cf. FIPS 180-2 Secure Hash Standard.
As most iterated hash functions, SHA-1 applies MD strengthening.
bits, cf. FIPS 180-2 Secure Hash Standard.
As most iterated hash functions, SHA-1 applies MD strengthening.
1.1 Compression Function
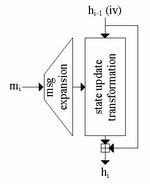
The compression function processes input message blocks of 512 bits and
produces a 160-bit chaining value. The compression function of
SHA-1 basically consists of two parts: the message expansion and
the state update transformation. The chaining variable 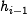 (iv in the first iteration) is added to the output of the state update transformation (feed forward).
(iv in the first iteration) is added to the output of the state update transformation (feed forward).
1.1.1 Message Expansion
In SHA-1, the message expansion is defined as follows. A single
512-bit input message block block is represented by 16 32-bit
words, denoted by 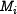 , with
, with 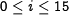 . The message input is linearly expanded into 80 32-bit words
. The message input is linearly expanded into 80 32-bit words 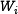 defined as follows:
defined as follows:
1.1.2 State Update Transformation
The state update transformation starts from a fixed initial value
iv for 5 32-bit registers 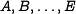 (also
referred to as state variables) and updates these registers in 80
steps (
(also
referred to as state variables) and updates these registers in 80
steps (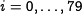 ) by using the word
) by using the word 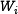 and the step
constant
and the step
constant 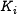 in step
in step 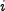 . One step of the state update transformation is defined as
. One step of the state update transformation is defined as
The function 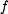 depends on the step number: steps
depends on the step number: steps 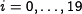 use the IF-function referred to as
use the IF-function referred to as 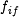 and steps
and steps 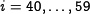 use the MAJ-function referred to as
use the MAJ-function referred to as 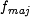 . The
remaining steps, use a 3-input XOR referred to as
. The
remaining steps, use a 3-input XOR referred to as 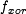 . The Boolean functions are defined as follows:
. The Boolean functions are defined as follows:
1.2 Padding Method
1.3 Constantsand Initial Value
1.3.1 Constants
1.3.2 Initial Value
2 Claimed/Expected Security Margins
3 Security Anaylsis
- Best know attack:
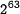 by Wang et.al.
by Wang et.al. - Best known collision example: 64-step collision by De Canniere and Rechberger
something like: best know attack to date: kind of attack, which variant has been looked at (e.g. round-reduced), complexity, and reference to paper and abstract.
may be make here a new page with the other cryptanalysis results.