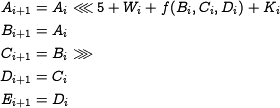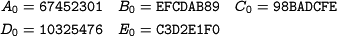Difference between revisions of "SHA-1"
(→Compression Function) |
(→Message Expansion) |
||
| Line 16: | Line 16: | ||
==== Message Expansion ==== | ==== Message Expansion ==== | ||
| − | The message | + | In SHA-1, the message expansion is defined as follows. A single |
| + | 512-bit input message block block is represented by 16 32-bit | ||
| + | words, denoted by <math>M_i</math>, with <math>0 \leq i \leq 15</math>. The message input is linearly expanded into 80 32-bit words <math>W_i</math> defined as follows: | ||
<amsmath> | <amsmath> | ||
| Line 27: | Line 29: | ||
\end{equation*} | \end{equation*} | ||
</amsmath> | </amsmath> | ||
| − | |||
==== State Update Transformation ==== | ==== State Update Transformation ==== | ||
Revision as of 09:41, 12 October 2006
Contents
1 General Description
SHA-1 is an iterated hash function. It can be used to
compute a 160-bit hash value for messages having a length of less
than 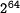 bits, cf. FIPS 180-2 Secure Hash Standard.
As most iterated hash functions, SHA-1 applies MD strengthening.
bits, cf. FIPS 180-2 Secure Hash Standard.
As most iterated hash functions, SHA-1 applies MD strengthening.
1.1 Compression Function
The compression function processes input message blocks of 512 bits and
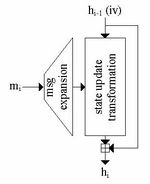
produces a 160-bit chaining value. The compression function of
SHA-1 basically consists of two parts: the message expansion and
the state update transformation. The chaining variable 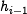 (iv in the first iteration) is added to the output of the state update transformation (feed forward).
(iv in the first iteration) is added to the output of the state update transformation (feed forward).
1.1.1 Message Expansion
In SHA-1, the message expansion is defined as follows. A single 512-bit input message block block is represented by 16 32-bit words, denoted by <math>M_i</math>, with <math>0 \leq i \leq 15</math>. The message input is linearly expanded into 80 32-bit words <math>W_i</math> defined as follows:
1.1.2 State Update Transformation
1.2 Padding Method
1.3 Constantsand Initial Value
1.3.1 Constants
1.3.2 Initial Value
2 Claimed/Expected Security Margins
3 Security Anaylsis
- Best know attack:
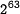 by Wang et.al.
by Wang et.al. - Best known collision example: 64-step collision by De Canniere and Rechberger
something like: best know attack to date: kind of attack, which variant has been looked at (e.g. round-reduced), complexity, and reference to paper and abstract.
may be make here a new page with the other cryptanalysis results.